Хорватія 🇭🇷
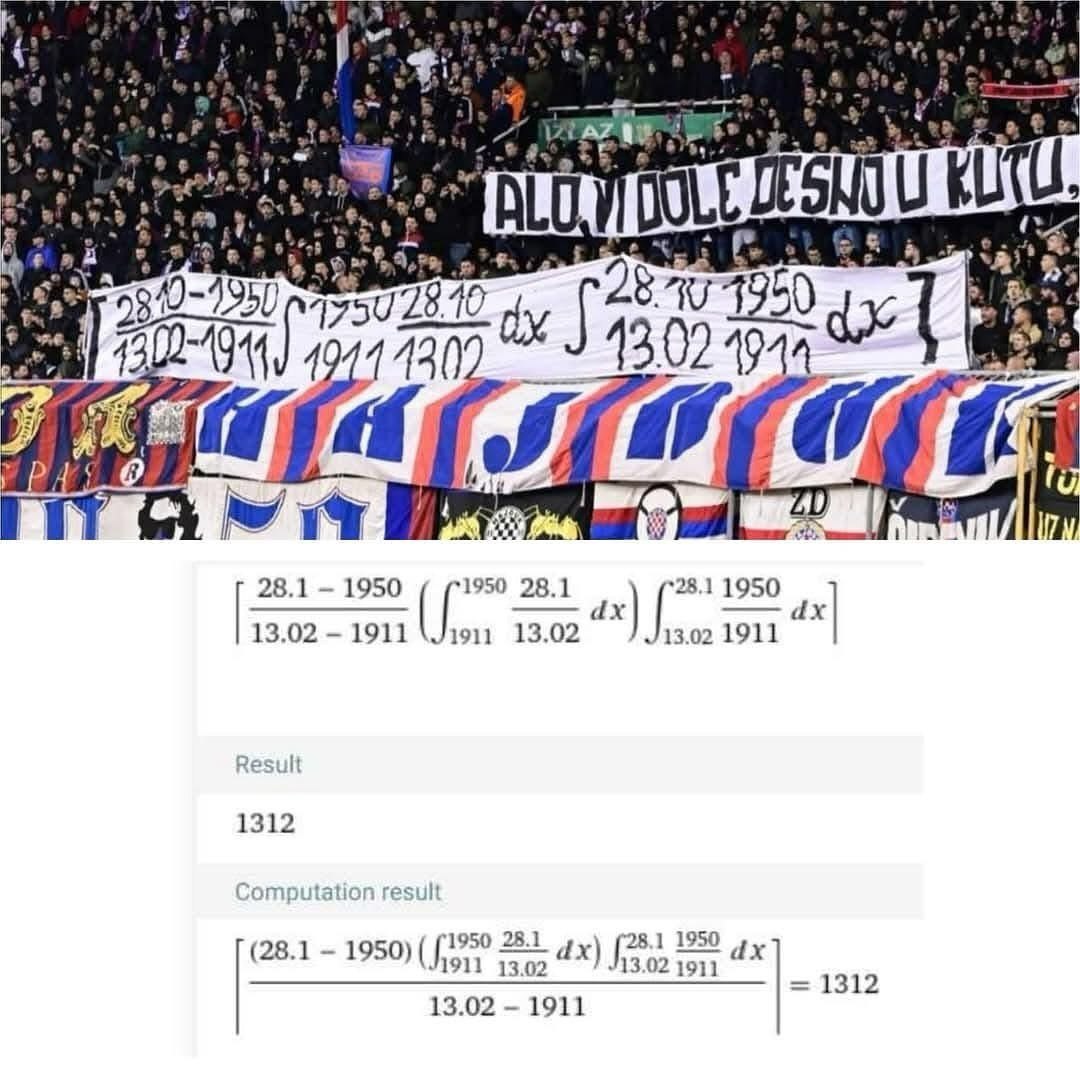
Сектори "Хайдука" на недільному матчі проти "Рієки" та їхній текстовик, на якому зображено математичне рівняння з інтегралами.
В основі формули бачимо важливі для хорватського клубу дати, а саме дату заснування "Хайдука" (13 лютого 1911), а також фанатського руху «Torcida Split» (28 жовтня 1950). Результатом розв'язання є число 1312, адресоване копам, що слідкують за фанатською трибуною з кута стадіону «Полюд».
Інтеграл є узагальненим поняттям суми нескінченного числа нескінченно малих доданків. Одне з найважливіших понять математичного аналізу, центральне поняття інтегрального числення, застосовується для розв'язання задач:
- обчислення площі під кривою;
- пройденого шляху за нерівномірного руху;
- маси неоднорідного тіла, і таке інше;
- відновлення функції за її похідною (невизначений інтеграл).
Основне досягнення в галузі інтегрування відбулося в 17-му столітті з відкриттям фундаментальної теореми числення (відомої як формула Ньютона — Ляйбніца) Ньютоном і Ляйбніцом, незалежно один від одного. Теорема встановлює зв'язок між інтегруванням і диференціюванням. Зокрема, основоположна теорема числення, дозволила розв'язувати ширший клас задач.
Ньютон і Ляйбніц створили комплексну математичну теорію, що є не менш важливим. Ця теорія має назву "Числення нескінченно малих величин", і дозволила здійснювати точний аналіз безперервних функцій. Ці засадничі роботи, зрештою стали сучасним численням, у якому була використана нотація для інтегралів, що безпосередньо спирається на роботи Лейбніца.
Знак інтеграла (∫) був уперше використаний Ляйбніцом наприкінці 17 століття. Це позначення, утворилося з букви ſ («довга s») від скорочення слова лат. ſumma (summa, сума).
Сектори "Хайдука" на недільному матчі проти "Рієки" та їхній текстовик, на якому зображено математичне рівняння з інтегралами.
В основі формули бачимо важливі для хорватського клубу дати, а саме дату заснування "Хайдука" (13 лютого 1911), а також фанатського руху «Torcida Split» (28 жовтня 1950). Результатом розв'язання є число 1312, адресоване копам, що слідкують за фанатською трибуною з кута стадіону «Полюд».
Інтеграл є узагальненим поняттям суми нескінченного числа нескінченно малих доданків. Одне з найважливіших понять математичного аналізу, центральне поняття інтегрального числення, застосовується для розв'язання задач:
- обчислення площі під кривою;
- пройденого шляху за нерівномірного руху;
- маси неоднорідного тіла, і таке інше;
- відновлення функції за її похідною (невизначений інтеграл).
Основне досягнення в галузі інтегрування відбулося в 17-му столітті з відкриттям фундаментальної теореми числення (відомої як формула Ньютона — Ляйбніца) Ньютоном і Ляйбніцом, незалежно один від одного. Теорема встановлює зв'язок між інтегруванням і диференціюванням. Зокрема, основоположна теорема числення, дозволила розв'язувати ширший клас задач.
Ньютон і Ляйбніц створили комплексну математичну теорію, що є не менш важливим. Ця теорія має назву "Числення нескінченно малих величин", і дозволила здійснювати точний аналіз безперервних функцій. Ці засадничі роботи, зрештою стали сучасним численням, у якому була використана нотація для інтегралів, що безпосередньо спирається на роботи Лейбніца.
Знак інтеграла (∫) був уперше використаний Ляйбніцом наприкінці 17 століття. Це позначення, утворилося з букви ſ («довга s») від скорочення слова лат. ſumma (summa, сума).
